Mystery Roulette Strategy
Introduction
When choosing a strategy/system, keep in mind that roulette odds are based on hypothetical, long-term sessions where each number on the roulette wheel is eventually selected an equal number of times. Experienced gamblers know that sessions played in real life certainly don't always play out as the odds predict they should. Many worthless betting strategies and systems are based on belief in the Gambler's Fallacy. I got the idea for writing about this after reading an 888 online roulette article by Frank Scoblete entitled How to Take Advantage of Roulette Hot Spots. In that article, Scoblete recommends taking a count of each outcome for 3,700 spins in single-zero.
The Gambler's Fallacy is the mistaken belief that if an independent event has not happened in a long time, then it becomes overdue and more likely. It is also equally incorrect that if an outcome has happened a disproportionate number of times lately, compared to statistical expectations, then it becomes overheated and less likely to occur the next time. An example of this fallacious thinking might be that if the number 23 hasn't been drawn in a 6-49 lottery the last 100 games, then it becomes more likely to be drawn during the next drawing.
Many worthless betting strategies and systems are based on belief in the Gambler's Fallacy. I got the idea for writing about this after reading an 888 online roulette article by Frank Scoblete entitled How to Take Advantage of Roulette Hot Spots. In that article, Scoblete recommends taking a count of each outcome for 3,700 spins in single-zero roulette and 3,800 spins in double-zero roulette in the hunt for 'hot numbers.' Never mind that this would take about 100 hours to make this many observations, assuming the industry standard of 38 spins per hour.
Before going further, let me say that I strongly believe modern roulette wheels made by top brands like Cammegh are extremely precise and any bias would be minuscule compared to the house advantage. Thus, testing a modern roulette for bias would be a total waste of time. Now, testing a 30-year-old hand-me-down wheel in a banana republic might be another story. However, you're on your own if you win a lot of money from said casino and try to leave with it.
That said, if you track 3,800 outcomes in single-zero roulette, the average number of times any number will hit is 3800/38=100. I ran a simulation of over 1.3 trillion spins, counting how many times each number was hit, sorting the outcomes to find the most frequent number and how many times it was observed, and keeping a count of how many times the most frequent number in each simulation was seen.

Hottest Number in 3,800 Spins of Double-Zero Roulette
As a former actuary, I hate to use a layman's term like the 'hottest number,' but that is how gamblers talk so will go with that. That said, following are the results of the count of the hottest number in millions of 3800-spin simulations.
Count of the Hottest Number in 3,800 Spins on Double-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 122.02 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
Here is what the table above means in plain simple English.
- The mean, or average, count of the hottest number is 122.02.
- The median count of the most frequent number is 121. This means that over 50% of time the most frequent number appeared 121 times or less, as well as 121 times or more. This is possible because the probability of 121 observations is in both groups.
- The mode, or most count of the hottest number is 120, which happens 8.29% of the time.
- The 90th percentile is the smallest number such that the probability the count of the hottest number is at least 90% .
- The 95th percentile is the smallest number such that the probability the count of the hottest number is at least 95%.
- The 99th percentile is the smallest number such that the probability the count of the hottest number is at least 99%.
- The 99.9th percentile is the smallest number such that the probability the count of the hottest number is at least 99.9%.
Hottest Number in 3,700 Spins of Single-Zero Roulette
The results are very similar with 3,700 spins tracked on a single-zero wheel. Following is a summary of the results.
Count of the Hottest Number in 3,700 Spins on Single-Zero Wheel
| Statistic | Value |
|---|---|
| Mean | 121.90 |
| Median | 121 |
| Mode | 120 |
| 90th Percentile | 128 |
| 95th Percentile | 131 |
| 99th Percentile | 136 |
| 99.9th Percentile | 142 |
The following table shows the full results of the simulation on both wheels. The two commulative columns show the probability that the count of the hottest number is the number on the left column or more. For example, the probability the hottest number in 3,700 spins of single-zero roulette is 130 or more is 0.072044.
Summary of the Count of the Hottest Number in 3,700 Spins of Single-Zero Roulette and 3,800 spins of Double-Zero Roulette
| Count | Probability Single Zero | Cummulative Single Zero | Probability Double Zero | Cummulative Double Zero |
|---|---|---|---|---|
| 160 or More | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 159 | 0.000000 | 0.000001 | 0.000000 | 0.000001 |
| 158 | 0.000001 | 0.000001 | 0.000001 | 0.000001 |
| 157 | 0.000001 | 0.000002 | 0.000001 | 0.000002 |
| 156 | 0.000001 | 0.000003 | 0.000001 | 0.000003 |
| 155 | 0.000002 | 0.000005 | 0.000002 | 0.000005 |
| 154 | 0.000003 | 0.000009 | 0.000003 | 0.000008 |
| 153 | 0.000005 | 0.000013 | 0.000005 | 0.000013 |
| 152 | 0.000007 | 0.000020 | 0.000008 | 0.000021 |
| 151 | 0.000012 | 0.000032 | 0.000012 | 0.000033 |
| 150 | 0.000017 | 0.000049 | 0.000018 | 0.000051 |
| 149 | 0.000026 | 0.000075 | 0.000027 | 0.000077 |
| 148 | 0.000038 | 0.000114 | 0.000041 | 0.000118 |
| 147 | 0.000060 | 0.000174 | 0.000062 | 0.000180 |
| 146 | 0.000091 | 0.000265 | 0.000092 | 0.000273 |
| 145 | 0.000132 | 0.000397 | 0.000137 | 0.000409 |
| 144 | 0.000195 | 0.000592 | 0.000199 | 0.000608 |
| 143 | 0.000282 | 0.000874 | 0.000289 | 0.000898 |
| 142 | 0.000409 | 0.001283 | 0.000421 | 0.001319 |
| 141 | 0.000580 | 0.001863 | 0.000606 | 0.001925 |
| 140 | 0.000833 | 0.002696 | 0.000860 | 0.002784 |
| 139 | 0.001186 | 0.003882 | 0.001215 | 0.003999 |
| 138 | 0.001652 | 0.005534 | 0.001704 | 0.005703 |
| 137 | 0.002315 | 0.007849 | 0.002374 | 0.008077 |
| 136 | 0.003175 | 0.011023 | 0.003286 | 0.011363 |
| 135 | 0.004355 | 0.015378 | 0.004489 | 0.015852 |
| 134 | 0.005916 | 0.021295 | 0.006088 | 0.021940 |
| 133 | 0.007939 | 0.029233 | 0.008196 | 0.030136 |
| 132 | 0.010601 | 0.039834 | 0.010908 | 0.041044 |
| 131 | 0.013991 | 0.053824 | 0.014384 | 0.055428 |
| 130 | 0.018220 | 0.072044 | 0.018757 | 0.074185 |
| 129 | 0.023498 | 0.095542 | 0.024114 | 0.098299 |
| 128 | 0.029866 | 0.125408 | 0.030603 | 0.128901 |
| 127 | 0.037288 | 0.162696 | 0.038228 | 0.167130 |
| 126 | 0.045771 | 0.208467 | 0.046898 | 0.214027 |
| 125 | 0.055165 | 0.263632 | 0.056310 | 0.270337 |
| 124 | 0.064853 | 0.328485 | 0.066020 | 0.336357 |
| 123 | 0.074178 | 0.402662 | 0.075236 | 0.411593 |
| 122 | 0.081929 | 0.484591 | 0.082885 | 0.494479 |
| 121 | 0.087158 | 0.571750 | 0.087696 | 0.582174 |
| 120 | 0.088520 | 0.660269 | 0.088559 | 0.670734 |
| 119 | 0.084982 | 0.745252 | 0.084406 | 0.755140 |
| 118 | 0.076454 | 0.821705 | 0.075245 | 0.830385 |
| 117 | 0.063606 | 0.885312 | 0.061851 | 0.892236 |
| 116 | 0.048069 | 0.933381 | 0.046111 | 0.938347 |
| 115 | 0.032432 | 0.965813 | 0.030604 | 0.968952 |
| 114 | 0.019117 | 0.984930 | 0.017664 | 0.986616 |
| 113 | 0.009567 | 0.994496 | 0.008614 | 0.995230 |
| 112 | 0.003894 | 0.998390 | 0.003420 | 0.998650 |
| 111 | 0.001257 | 0.999647 | 0.001065 | 0.999715 |
| 110 | 0.000297 | 0.999944 | 0.000243 | 0.999958 |
| 109 | 0.000050 | 0.999994 | 0.000038 | 0.999996 |
| 108 or Less | 0.000006 | 1.000000 | 0.000004 | 1.000000 |
Count of the Hottest Numbers in 300 Spins in Double-Zero Roulette
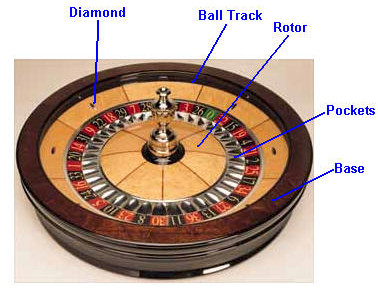
What if you don't want to spend 100 hours gathering data on a single wheel? Some casinos are kind enough to give you, on a silver platter, the number of times in the last 300 spins the four 'hottest' and 'coolest' numbers occurred. The image at the top of the page shows an example taken on a double-zero wheel at the Venetian.
In 300 spins, the average number of wins on a double-zero wheel for any number is 300/38=7.9. As you can see from the image above, the four hottest numbers were 20, 5, 29, and 2, which occurred 15, 14, 13, and 12 times respectively. Is this unusual? No. In a simulation of over 80 billion spins, the most frequent number, in 300-spin experiments, appeared most frequently at 14 times with a probability of 27.4%. The most likely total of the second, third, and fourth most frequent numbers was 13, 12, and 12 times respectively, with probabilities of 37.9%, 46.5%, and 45.8%. So the results of the 'hottest' numbers in the image above were a little more flat than average.
The following table shows the probabilities of the four hottest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.009210.

Count of the Hottest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Most Frequent | Probability Second Most Frequent | Probability Third Most Frequent | Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000022 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000051 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000166 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000509 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.001494 | 0.000001 | 0.000000 | 0.000000 |
| 20 | 0.004120 | 0.000009 | 0.000000 | 0.000000 |
| 19 | 0.010806 | 0.000075 | 0.000000 | 0.000000 |
| 18 | 0.026599 | 0.000532 | 0.000003 | 0.000000 |
| 17 | 0.060526 | 0.003263 | 0.000060 | 0.000001 |
| 16 | 0.123564 | 0.016988 | 0.000852 | 0.000020 |
| 15 | 0.212699 | 0.071262 | 0.009210 | 0.000598 |
| 14 | 0.274118 | 0.215025 | 0.068242 | 0.011476 |
| 13 | 0.212781 | 0.379097 | 0.283768 | 0.117786 |
| 12 | 0.067913 | 0.270747 | 0.464748 | 0.457655 |
| 11 | 0.004615 | 0.042552 | 0.168285 | 0.383900 |
| 10 | 0.000017 | 0.000448 | 0.004830 | 0.028544 |
| 9 | 0.000000 | 0.000000 | 0.000001 | 0.000020 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary of the Count of the Four Most Frequent Numbers in 300 Spins of Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.48 | 14 | 14 |
| Second | 13.07 | 13 | 13 |
| Third | 12.27 | 12 | 12 |
| Fourth | 11.70 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Double-Zero Roulette
The next table shows the probability of each count of the four collest numbers in 300 spins of double-zero roulette.
Mystery Card Roulette Strategy
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent | Probability Second Least Frequent | Probability Third Least Frequent | Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.012679 | 0.000063 | 0.000000 | 0.000000 |
| 1 | 0.098030 | 0.005175 | 0.000135 | 0.000002 |
| 2 | 0.315884 | 0.088509 | 0.012041 | 0.001006 |
| 3 | 0.416254 | 0.420491 | 0.205303 | 0.063065 |
| 4 | 0.150220 | 0.432638 | 0.595139 | 0.522489 |
| 5 | 0.006924 | 0.052945 | 0.185505 | 0.401903 |
| 6 | 0.000008 | 0.000180 | 0.001878 | 0.011534 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of double-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.61 | 3 | 3 |
| Second Least | 3.44 | 3 | 4 |
| Third Least | 3.96 | 4 | 4 |
| Fourth Least | 4.36 | 4 | 4 |
Count of the Hottest Numbers in 300 Spins of Single-Zero Roulette
In 300 spins, the average number of wins on a single-zero wheel for any number is 300/37=8.11. The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third most frequent number happens 15 times is 0.015727.
Count of the Hottest Four Numbers in 300 Spins on a Single-Zero Wheel
| Observations | Probability Most Frequent | Probability Second Most Frequent | Probability Third Most Frequent | Probability Fourth Most Frequent |
|---|---|---|---|---|
| 25 or More | 0.000034 | 0.000000 | 0.000000 | 0.000000 |
| 24 | 0.000078 | 0.000000 | 0.000000 | 0.000000 |
| 23 | 0.000245 | 0.000000 | 0.000000 | 0.000000 |
| 22 | 0.000728 | 0.000000 | 0.000000 | 0.000000 |
| 21 | 0.002069 | 0.000002 | 0.000000 | 0.000000 |
| 20 | 0.005570 | 0.000018 | 0.000000 | 0.000000 |
| 19 | 0.014191 | 0.000135 | 0.000000 | 0.000000 |
| 18 | 0.033833 | 0.000905 | 0.000008 | 0.000000 |
| 17 | 0.074235 | 0.005202 | 0.000125 | 0.000001 |
| 16 | 0.144490 | 0.025286 | 0.001624 | 0.000050 |
| 15 | 0.232429 | 0.097046 | 0.015727 | 0.001286 |
| 14 | 0.269735 | 0.259360 | 0.101259 | 0.021054 |
| 13 | 0.177216 | 0.382432 | 0.347102 | 0.175177 |
| 12 | 0.043266 | 0.208137 | 0.429715 | 0.508292 |
| 11 | 0.001879 | 0.021373 | 0.102979 | 0.283088 |
| 10 | 0.000003 | 0.000103 | 0.001461 | 0.011049 |
| 9 | 0.000000 | 0.000000 | 0.000000 | 0.000002 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth hottest numbers in millions of 300-spin simulations of double-zero roulette.
Summary — Count of the Four Hottest Numbers — Double-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| First | 14.74 | 15 | 14 |
| Second | 13.30 | 13 | 13 |
| Third | 12.50 | 12 | 12 |
| Fourth | 11.92 | 12 | 12 |
Count of the Coolest Numbers in 300 Spins in Single-Zero Roulette
The next table shows the probability of each count of the four coolest numbers in 300 spins of double-zero roulette. For example, the probability the third coolest numbers will be observed five times is 0.287435.
Count of the Coolest Four Numbers in 300 Spins on a Double-Zero Wheel
| Observations | Probability Least Frequent | Probability Second Least Frequent | Probability Third Least Frequent | Probability Fourth Least Frequent |
|---|---|---|---|---|
| 0 | 0.009926 | 0.000038 | 0.000000 | 0.000000 |
| 1 | 0.079654 | 0.003324 | 0.000068 | 0.000001 |
| 2 | 0.275226 | 0.062392 | 0.006791 | 0.000448 |
| 3 | 0.419384 | 0.350408 | 0.140173 | 0.034850 |
| 4 | 0.200196 | 0.484357 | 0.557907 | 0.406702 |
| 5 | 0.015563 | 0.098547 | 0.287435 | 0.521238 |
| 6 | 0.000050 | 0.000933 | 0.007626 | 0.036748 |
| 7 | 0.000000 | 0.000000 | 0.000001 | 0.000013 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the mean, median, and mode for the count of the first, second, third, and fourth coolest numbers in the 300-spin simulations of single-zero roulette.
Summary of the count of the Four Least Frequent Numbers on a Single-Zero Wheel
| Order | Mean | Median | Mode |
|---|---|---|---|
| Least | 2.77 | 3 | 3 |
| Second Least | 3.62 | 4 | 4 |
| Third Least | 4.15 | 4 | 4 |
| Fourth Least | 4.56 | 5 | 5 |
The least I hope you have learned from this article is it is to be expected that certain numbers will come up more than others. To put it in other words, it is natural that some numbers will be 'hot' and some 'cool.' In fact, such differences from the mean are highly predictable. Unfortunately, for roulette players, we don't know which numbers will be 'hot,' just that some of them almost certainly will be. I would also like to emphasize, contrary to the Gambler's Fallacy, that on a fair roulette wheel that every number is equally likely every spin and it makes no difference what has happened in the past.
Finally, it should not be interpreted that we give an endorsement to the 888 Casino, which we linked to earlier. I am very bothered by this rule in their rule 6.2.B. Before getting to that, let me preface with a quote from rule 6.1, which I'm fine with.
'If we reasonably determine that you are engaging in or have engaged in fraudulent or unlawful activity or conducted any prohibited transaction (including money laundering) under the laws of any jurisdiction that applies to you (examples of which are set out at section 6.2 below), any such act will be considered as a material breach of this User Agreement by you. In such case we may close your account and terminate the User Agreement in accordance with section 14 below and we are under no obligation to refund to you any deposits, winnings or funds in your account.' -- Rule 6.1

Let's go further now:
The following are some examples of 'fraudulent or unlawful activity' -- Rule 6.2
Next, here is one of many examples listed as rule 6.2.B
'Unfair Betting Techniques: Utilising any recognised betting techniques to circumvent the standard house edge in our games, which includes but is not limited to martingale betting strategies, card counting as well as low risk betting in roulette such as betting on red/black in equal amounts.' -- Rule 6.2.B
Let me make it perfectly clear that all betting systems, including the Martingale, not only can't circumvent the house edge, they can't even dent it. It is very mathematically ignorant on the part of the casino to fear any betting system. Why would any player trust this casino when the casino can seize all their money under the reason that the player was using a betting system? Any form of betting could be called a betting system, including flat betting. Casino 888 normally has a pretty good reputation, so I'm surprised they would lower themselves to this kind of rogue rule.
Written by: Michael Shackleford
There are dozens of roulette betting strategies, including famous ones such as the Martingale or the D’Alembert systems which focus on the even-money outside bets. But there is one quite interesting betting system that differs from all the classic methods and it is called the Kavouras system. It is unique, aggressive and very chaotic at least at first sight but it is often described as the best, guaranteed way to win in roulette.
All this sounds very promising and would appeal to most gamblers, especially if they are new to roulette, one of the most exciting and elegant casino games ever created. So, what is the Kavouras strategy and is it really as successful as it claims to be? Unlike most casino betting systems that have been around for more than a century, it is quite a recent invention. It is named after its creator, a gambler known simply as Kavouras, who published the system in 2010. Interestingly, no detailed information is available about the roulette player and over the years, the betting system has been shrouded in mystery.
- Bonus⋆80 Free Spins
- Bonus$300
- $500$600
Today, it is fairly popular among the gambling community although few players admit to using it in land-based or online casinos. This could be attributed to the fact it is often described as quite expensive, chaotic, and absolutely outrageous compared to the rest of the betting systems, which are well-organized, methodical, and conservative. The reason why the Kavouras is considered to be an unorthodox betting system is that it requires the player to bet on 20 numbers that are positioned in no particular order on the wheel.

In fact, the strategy contains inside bets that have a low probability of winning and great payouts at the same time. For most players, such a system of bets would look counterintuitive because generally, the safest options when wagering on roulette are the outside bets and the vast majority of betting strategies focus on them. Still, the Kavouras gained a lot of popularity and is currently among the hottest and most discussed roulette systems. In the sections below, gamblers can find a complete description of it so they can decide for themselves whether it is worth applying and whether its claims hold merit.
The Concept of the Kavouras Strategy
The Kavouras strategy is a system of bets specifically designed for roulette. In contrast, the majority of betting systems can be applied to a wide variety of games where there are two, equally likely outcomes such as in flipping coins. This method, however, ditches the traditional wagering on even-money bets such as red/black, high/low, and even/odd, and instead, allows players to make inside bets. The idea is that these bets pay out much more than the typical 1:1 payout for red or black, for instance.
According to the professional roulette player Kavouras, roulette is random and based on pure chance, which means it is chaotic. Therefore, in order to be successful, the bets should also be chaotic. And they are – the system includes 20 numbers that are scattered around the roulette wheel in no particular order. This approach, according to the creator of the strategy, prevents any action on the dealer’s or the casino’s part that aims at leading the ball away from the sector chosen by the player.
Kavouras Strategy Additional TipsThe next important step is to keep the stake amount chaotic, too. The system achieves this by placing different numbers of chips on different selections of numbers. To be more specific, 2 chips are placed on a six line bet, 1 chip is placed on the basket bet, namely from 0 through 3, and another 5 chips are placed on five different splits. In total, players need to bet at least 8 chips on 20 numbers. The idea is to bet on as many numbers as possible for as little as possible and to keep applying this pattern until the ball falls on any of the five splits. Then, the 17:1 payout should be large enough to compensate for any previously lost funds.
The strategy claims that it wins every time and that winning is actually more likely than losing. According to the author of this system and some players who apply it, it manages to beat the odds and guarantees winnings over the long run because on every individual spin, there are 20 ways to win against only 17 ways to lose (or 18 in American roulette). Indeed, players can expect to win more times than lose.
How to Apply the Kavouras Strategy on Roulette?
When speaking of the strategy devised by Kavouras, we can describe it as a strategy, a system, or just as the Kavouras bet. Gamblers who decide to play roulette with this bet should know that it always remains the same – at least in terms of the numbers it covers. As mentioned above, a total of 8 chips are placed but the chip size could vary, depending on the table limits and the player’s individual bankroll. It could be worth $1, $5, $10 or more, so let’s refer to the preferred basic bet amount as a unit. The Kavouras pattern includes the following bets:
- 1 unit on 0-1-2-3 – the corner or basket bet pays 8:1, 1 unit profit
- 2 units on 31-32-33-34-35-36 – the six line bet pays 5:1, 4 units profit
- 5 units on 8-11, 13-14, 15-18, 17-20, 27-30 – the split bets pay 17:1, 10 units profit
Kavouras Strategy Additional TipsAs we can see, we bet 8 units on a total of 20 numbers with this system but the payout for each group of numbers is different. Therefore, the net profit will be different, too. Let’s say we place $8 with the Kavouras bet and the ball hits 32 red – for this particular number, we will receive $10 in winnings (5:1) plus the $2 stake placed on the six line. When we deduct the bet amount from the total amount, we get a net profit of $4. We can easily calculate the expected profit from the other bets in the same manner. It becomes obvious that whenever the Kavouras bet wins, the profit is 1, 4, or 10 units. When it loses, however, the net loss is 8 units.
Flat Kavouras Betting
Players are advised to start with the table minimum when determining the exact amount of the betting unit. They can opt for flat betting, i.e. keeping the amount of the bet the same, or choose a betting progression. The type of progression could be of any kind as long as it suits players’ individual bankrolls. Doubling the number of units every time is an option but it is too aggressive and risky. Besides, the three types of bets that are included in the pattern have different probabilities and payouts, so most players prefer to increase their value accordingly.
Below, we have demonstrated a random gaming session using flat bets. We have started with the minimum betting limit of $1, so each wager would cost $8.
| Spin | Bet | Outcome | Payout | Profit/Loss |
|---|---|---|---|---|
| 1 | $8 | Lose | $0 | -$8 |
| 2 | $8 | Win, split 17:1 | $18 | $2 |
| 3 | $8 | Win, split 17:1 | $18 | $12 |
| 4 | $8 | Lose | $0 | $4 |
| 5 | $8 | Win, split 17:1 | $18 | $14 |
| 6 | $8 | Lose | $0 | $6 |
| 7 | $8 | Win, split 17:1 | $18 | $16 |
| 8 | $8 | Lose | $0 | $8 |
| 9 | $8 | Win, corner 8:1 | $9 | $9 |
| 10 | $8 | Lose | $0 | $1 |
| 11 | $8 | Win, corner 8:1 | $9 | $2 |
| 12 | $8 | Win, split 17:1 | $18 | $12 |
| Total Bet Amount: | $96 | Total Payout: $108 | Net Profit: $12 |
Bet Progression with the Kavouras Strategy
As demonstrated in the example above, the Kavouras system could be very successful, yet just a few losses throughout our gaming session can easily cut down the profits. Players with a higher tolerance for risk and larger bankrolls have the option to address this problem by staking more on each following spin and make the most of their winning streaks. As the Kavouras bet covers most of the roulette table, it is already expensive and any further increase of the wagered amount should be done with caution.
When we want to apply some type of betting progression to this strategy, we start our gaming session with the basic 8-unit wager. The most common progression for the Kavouras bet continues with placing 18 units as follows – 3 units on the corner, 5 units on the six line, and 10 units on the five splits (2 units per split). The idea is to be able to generate bigger profits each time we win. The progression stops and we return to our initial bet following a loss.
Players with really high bankrolls can also continue with betting 8 units on the corner, 11 units on the six line, and 20 units on the splits. In total, the third bet would cost 39 units. Those who have reached this level are advised to stop the progression and return to their original 8-unit Kavouras bet, as any further increase is considered too risky. In the example below, we can see how the system would like with only a medium level of risk where we increase the bet just once and continue with flat bets until we lose.
| Spin | Bet | Outcome | Payout | Profit/Loss |
|---|---|---|---|---|
| 1 | $8 | Lose | $0 | -$8 |
| 2 | $8 | Win, split 17:1 | $18 | $2 |
| 3 | $18 | Win, split 17:1 | $36 | $20 |
| 4 | $18 | Win, split 17:1 | $36 | $38 |
| 5 | $18 | Win, six line 5:1 | $30 | $50 |
| 6 | $18 | Lose | $0 | $32 |
| 7 | $8 | Lose | $0 | $24 |
| 8 | $8 | Lose | $0 | $16 |
| 9 | $8 | Lose | $0 | $8 |
| 10 | $8 | Lose | $0 | 0 |
| 11 | $8 | Win, six line 5:1 | $12 | $4 |
| 12 | $18 | Win, split 17:1 | $36 | $22 |
| Total Bet Amount: | $146 | Total Payout: $168 | Net Profit: $22 |
Can the Kavouras Strategy Beat the Odds?
The Kavouras strategy is considered by some players to be the best system for roulette right now because by covering most of the numbers on the roulette wheel, it effectively beats the odds. This sounds true – with this bet, gamblers play with 20 numbers, which means they have 20 ways to win and 17 ways to lose on each spin (we will take the single-zero European and French roulette games for this example). In reality, the Kavouras bet covers 54% of the wheel and winning spins are expected to occur more often than losing ones.
Indeed, the system does beat the odds – usually, the best odds in roulette are for the even-money bets which have a probability of winning of 48.65% and odds of 19 to 18 against the player. Here, the odds are in players’ favor, 20:17, while the probability of winning is 20/37 or 54.05%. But no strategy or betting pattern can actually beat the house advantage, which is much more important as it takes into account the payout offered by the casino for each bet.
In reality, in order for the Kavouras bet or any other bet for that matter to be effectively guaranteeing winnings over the long run, it should be advantageous to the player and not the casino. The house edge is the precise indication of this as it compares the true odds of a bet, the payout offered if it wins, and the actual probability of winning. Players can calculate the house edge of the different types of bets that form the Kavouras pattern, using the following formula:
House Edge = (True Odds – Casino Odds) * Probability
Let us see the expected value (this is the opposite of the house edge, the same number but with a negative sign) of any of the split bets that are placed as part of the Kavouras system. The true odds of a split are 35/2, where 35 indicates the numbers of ways to lose this bet, while the 2 corresponds to the numbers of ways we can win the bet. The casino odds, on the other hand, are the funds offered as a reward if we win a split bet, or 17/1 (17:1). The probability is equally easy to get – it is the ratio between the ways to win and all possible ways. In this case, we have 2 winning numbers out of 37, so the probability is 2/37. The house edge for the split bet can, therefore, be calculated like this:
House Edge = (35/2-17/1)*2/37 = 0.5*0.05405405405 = 0.02702702702
In order to express the casino’s advantage as a percentage, we simply multiply this number by 100 and we get 2.70%, which is exactly the house edge of European roulette. We can calculate the house edge for the rest of the bets in the pattern and every time, we will get that exact same percentage. This proves that while the Kavouras system may be winning in terms of the number of wins, it is not profitable in the long term due to the casino advantage built in the payouts of the bets.
The house edge suggests that out of every $100 wagered in European roulette, the casino keeps $2.70. Players who bet $100 in American roulette, on the other hand, can expect to lose $5.26 on average since the house advantage there is 5.26%.
Advantages and Disadvantages of the Kavouras Strategy
After learning how it works and the mathematics behind it, roulette players are now probably wondering whether the Kavouras bet is worth using or not. As with all other strategies for roulette, this system has its strengths and weaknesses that should be considered very carefully. One of its unique aspects is that it is not an even-money bet system but a combination of several inside bets. When winning, these wagers are much more profitable than the black/red, high/low, and even/odd bets that are typically being placed in most roulette strategies.
And with the Kavouras pattern, players certainly hit more winning spins than losing ones, which is probably the biggest advantage of using this particular betting system. As the pattern covers more than half of the numbers on the wheel (20 out of 37), wins will be more than losses. Of course, another great thing about the Kavouras is that it is extremely simple and easy to apply on the roulette table once you learn the pattern. Nothing changes in the system, except for the optional betting progression, so after a few spins, most players should be able to remember it.
Advantages and DisadvantagesIf used more conservatively with flat bets, the Kavouras strategy is relatively safe and reliable. If the bet wins, it always turns a profit – 1, 4, or 10 units, and if it loses, the player loses 8 units. While this may not be too much at first, this loss could be hard for players to recover from if they hit a six line bet or a corner as the profit from these would not be enough to cover the 8-unit loss. Things could escalate even more if a losing streak occurs.
This is, in fact, the biggest downside to the Kavouras system – that it generates decent profits while the player is winning but as soon as several consecutive losing spins are registered, the player’s bankroll is in real danger. The only way to regain the losses is hitting several splits in a row, which although being possible, is not very probable. The real trouble starts when the player decides to adopt a betting progression together with the strategy and experiences a losing streak.
Mystery Card Roulette Strategy
Conclusion
The Kavouras strategy is certainly one of the most interesting and entertaining roulette systems in existence and it enjoys great popularity among both casino veterans and complete novices. It is easy to apply online and in land-based casinos and it provides great coverage at the lowest possible price. Of course, there are other strategies that allow you to bet on large sectors of the roulette wheel but the Kavouras differs significantly as the numbers it includes are arranged chaotically on the wheel.
Overall, this is a good and fun strategy that allows players to make their game more diverse, riskier and potentially rewarding. It is suitable for those who are already familiar with the game and are looking for an interesting and smart approach that can actually bring them nice profits. High-rollers may also opt for increasing the total amount of the stake in order to maximize their winnings and make the game a little more thrilling.